So, I am now thoroughly confused! I now think that perhaps the version of the Solow model outlined in my previous
post is actually an Ergodic model! I think this despite the fact that the deterministic version of the same model is (I think) non-Ergodic because it has multiple steady-states and long-run outcomes are completely dependent on initial conditions of capital stock.
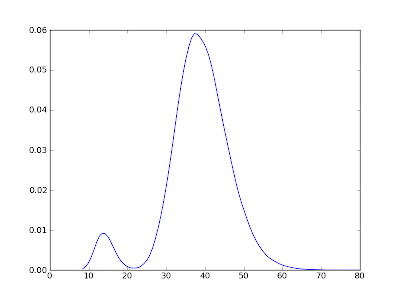
Below are estimates of the unique pdf and cdf of steady-state distribution of the Solow model from my previous post (with identical parameter values). John Stachurksi, in his book
Economic Dynamics
proves that the model is globally stable and thus that the steady-state distribution is unique. Global stability, I think, implies that a process is Ergodic. The distribution was created by simulating the model for 100,000 periods and then estimating the pdf using non-parametric kernel density estimation. The cdf was estimated using an estimator based on the empirical cdf.
Threshold Solow PDF:
Note that the distribution is double-humped. The reason that the left-hand hump (corresponding to the "poor" attractor) is small relative to the right-hand hump is that the threshold level of capital stock,
kb, is such that once the economy moves into the "rich" attractor's basin it is unlikely to get shocked out. If you where to raise the threshold
kb, then the left-hand hump would get bigger.
Threshold Solow CDF:
As promised, I will post a link to Github later today with the Python code...

The stochastic version of the model is ergodic. Sketch proof: Recall that the process is ergodic iff every invariant set of trajectories has probability 0 or 1. For it to be non-ergodic, there must exist at least two invariant sets of trajectories of positive probability. Suppose that were true. Because the model is a Markov process, invariant sets of trajectories would imply two sets in the state space, call them F and G, of positive probability, such the probability of going from F to G and from G to F was zero. But, because of the log-normal noise, the probability of going from any state to any set is positive. Hence, not non-ergodic, therefore, ergodic.
ReplyDeleteOf course, the time-scale needed to move from one not-quite-steady-state to the other is a different story.
Cosma,
ReplyDeleteOnce again, thanks for clearing up the confusion. I must say that I didn't suspect it to be the case that adding noise to a non-ergodic system could make it ergodic...but upon a bit more reflection (and going through the exercise of programming this version of the Solow model) it seems slightly intuitive.
Adding enough randomness allows the system to "jump" out of what had previously been an absorbing state. By "enough" I mean that I assume that there is some shock distributions for which this model would still be non-ergodic.
Log-normal is a heavy-tailed distribution, so perhaps the model would still non-ergodic with normal noise (or maybe some bounded noise distribution)...
Normal noise won't work because there is still positive probability of drawing an arbitrarily high shock. I think the model will be non-ergodic with some bounded noise distribution. Suppose the upper bound on W is W'>1, and suppose that starting at some k_0 in [0,k_b), we draw a series of shocks W', W', ... Then the model will behave exactly like the deterministic Solow model with savings rate sW'. The economy will move towards to the steady state associated with this savings rate, say k*(W'). If k*(W') is less than the threshold level of the capital stock k_b, the economy will stay at k*(W'). (If k*(W')>k_b, of course, the economy will tip over the threshold.) Because the shocks are bounded, any possible sequence of shocks must be weakly smaller, term by term, than the sequence W', W', ... considered here. Because the system is monotonic in W, this means that the trajectory generated by this sequence of shocks will be lower than the trajectory just considered, and so it cannot reach a point above k_b. So for any W' such that k*(W')<k_b, the probability of going from the set [0,k_b) to the set (k_b,\infty) is zero. (By a similar argument, we can find a lower bound on W such that the converse is true.)
ReplyDeleteThis would not work if the shocks were additive, i.e. if k_{t+1} = sA_t k_t^a + (1-d)k_t + W_t. Then, even with a bounded W, there would always be a positive probability of reaching any point starting at any other point, e.g. using a long enough sequence W', W',... (at least over the region where k_{t+1} is increasing in k_t).
Keshav,
ReplyDeleteThanks for the excellent comment! The observation that adding noise can turn a non-ergodic system into and ergodic one seems an important one...also it was a priori unexpected (for me at least) but ex post seemed completely obvious...
In a way it's kind of like simulated annealing optimization...things can improve quite a bit with a splash of randomness! If indeed taking a non-ergodic process and making it ergodic is in fact an improvement.
A rough heuristic for this sort of thing is this. Start with the deterministic model, and find its basins of attraction and attractors. Now add in the noise: does it give a positive probability of moving from the vicinity of one attractor to the other basin of attraction? So here I think it's enough that the distribution of the noise have support on the whole real line.
ReplyDelete