I recently wrote some Python code to compute paths of technology and the implied Solow residuals using data from the Penn World Tables. Combining the results with some country metadata (i.e., income groupings) from the World Bank API yields this pretty interesting graphic...
If you don't already have the Penn World Tables data...no worries! The script will download the PWT data, compute the Solow residuals based on a method used by Hall and Jones (1999). Based on this decomposition, high income (i.e., red) countries had higher levels of technology in 1960 and higher subsequent growth rates of technology. In fact, the low income (i.e., purple) countries have had effectively zero technological progress since 1960!
Enjoy!
Blog Topics...
3D plotting
(1)
Academic Life
(2)
ACE
(18)
Adaptive Behavior
(2)
Agglomeration
(1)
Aggregation Problems
(1)
Asset Pricing
(1)
Asymmetric Information
(2)
Behavioral Economics
(1)
Breakfast
(4)
Business Cycles
(8)
Business Theory
(4)
China
(1)
Cities
(2)
Clustering
(1)
Collective Intelligence
(1)
Community Structure
(1)
Complex Systems
(42)
Computational Complexity
(1)
Consumption
(1)
Contracting
(1)
Credit constraints
(1)
Credit Cycles
(6)
Daydreaming
(2)
Decision Making
(1)
Deflation
(1)
Diffusion
(2)
Disequilibrium Dynamics
(6)
DSGE
(3)
Dynamic Programming
(6)
Dynamical Systems
(9)
Econometrics
(2)
Economic Growth
(5)
Economic Policy
(5)
Economic Theory
(1)
Education
(4)
Emacs
(1)
Ergodic Theory
(6)
Euro Zone
(1)
Evolutionary Biology
(1)
EVT
(1)
Externalities
(1)
Finance
(29)
Fitness
(6)
Game Theory
(3)
General Equilibrium
(8)
Geopolitics
(1)
GitHub
(1)
Graph of the Day
(11)
Greatest Hits
(1)
Healthcare Economics
(1)
Heterogenous Agent Models
(2)
Heteroskedasticity
(1)
HFT
(1)
Housing Market
(2)
Income Inequality
(2)
Inflation
(2)
Institutions
(2)
Interesting reading material
(2)
IPython
(1)
IS-LM
(1)
Jerusalem
(7)
Keynes
(1)
Kronecker Graphs
(3)
Krussel-Smith
(1)
Labor Economics
(1)
Leverage
(2)
Liquidity
(11)
Logistics
(6)
Lucas Critique
(2)
Machine Learning
(2)
Macroeconomics
(45)
Macroprudential Regulation
(1)
Mathematics
(23)
matplotlib
(10)
Mayavi
(1)
Micro-foundations
(10)
Microeconomic of Banking
(1)
Modeling
(8)
Monetary Policy
(4)
Mountaineering
(9)
MSD
(1)
My Daily Show
(3)
NASA
(1)
Networks
(46)
Non-parametric Estimation
(5)
NumPy
(2)
Old Jaffa
(9)
Online Gaming
(1)
Optimal Growth
(1)
Oxford
(4)
Pakistan
(1)
Pandas
(8)
Penn World Tables
(1)
Physics
(2)
Pigouvian taxes
(1)
Politics
(6)
Power Laws
(10)
Prediction Markets
(1)
Prices
(3)
Prisoner's Dilemma
(2)
Producer Theory
(2)
Python
(29)
Quant
(4)
Quote of the Day
(21)
Ramsey model
(1)
Rational Expectations
(1)
RBC Models
(2)
Research Agenda
(36)
Santa Fe
(6)
SciPy
(1)
Shakshuka
(1)
Shiller
(1)
Social Dynamics
(1)
St. Andrews
(1)
Statistics
(1)
Stocks
(2)
Sugarscape
(2)
Summer Plans
(2)
Systemic Risk
(13)
Teaching
(16)
Theory of the Firm
(4)
Trade
(4)
Travel
(3)
Unemployment
(9)
Value iteration
(2)
Visualizations
(1)
wbdata
(2)
Web 2.0
(1)
Yale
(1)
Saturday, January 26, 2013
Thursday, January 24, 2013
Solving models with heterogenous agents...
This material was previously part of another post on welfare costs of business cycles. I decided that the links on solving Krusell-Smith deserved its own post!
Place to start is definitely Wouter den Haan's website, specifically his introductory slides on heterogenous agent models. Krusell and Smith (2006) is an excellent literature review on heterogenous agent models.
Various solution algorithms: Key difficulty in solving Krusell-Smith type models is to find a way to summarize the cross-sectional distribution of capital and employment status (a potentially infinite dimensional object) with a limited set of its moments.
- Original KS algorithm: The KS algorithm specifies a law of motion for these moments and then finds the approximating function to this law of motion using a simulation procedure. Specifically, for a given a set of individual policy rules (which can be solved for via value function iterations, etc), a time series of cross-sectional moments is generated and new laws of motion for the aggregate moments are estimated using this simulated data.
- Xpa algorithm
- Other algorithms
Den Haan (2010):
This paper compares numerical solutions to the model of Krusell and Smith [1998. Income and wealth heterogeneity in the macroeconomy. Journal of Political Economy 106, 867–896] generated by different algorithms. The algorithms have very similar implications for the correlations between different variables. Larger differences are observed for (i) the unconditional means and standard deviations of individual variables, (ii) the behavior of individual agents during particularly bad times, (iii) the volatility of the per capita capital stock, and (iv) the behavior of the higher-order moments of the cross-sectional distribution. For example, the two algorithms that differ the most from each other generate individual consumption series that have an average (maximum) difference of 1.63% (11.4%).Concise description of Krusell and Smith (1998) model can be found in the introduction to the JEDC Krusell-Smith comparison project. It would seem the JEDC Krusell-Smith comparison project is a good place to start thinking about how to implement the Krusell-Smith algorithm in Python. The above paper suggests that implementation details matter and can substantially impact the accuracy of solution. Wouter den Haan provides code for JECD comparison project. Maybe start by implementing the den Haan and Rendahl (2009) algorithm in Python? Followed by Reiter (2009). Given that different algorithms can arrive at different solutions, checking the accuracy of a given solution method against alternatives is important. Slides on the checking accuracy of the above algorithms.
Other Krusell-Smith related links:
- Anthony Smith's original Fortran implementation of Krusell-Smith. Code looks completely impenetrable! Not much in the way of comments or documentation. Probably not worth working out how the code works.
- Sergei Mailar's MatLab code for Krusell-Smith (Mailar provides code for other interesting projects as well!).
- Fortran code for Krusell and Smith (2009).
- Wouter den Haan's slides on additional applications of the Krusell-Smith approach (includes monetary models with consumer heterogeneity, models with entrepreneurs, turning KS into a matching model, portfolio problem).
Thursday, January 17, 2013
Python code to grab Penn World Tables data
For any interested parties, I wrote a small python script to download the Penn World Tables dataset and convert it into a Pandas Panel. Code passed all of my tests, but can't claim that it is industrial strength.
To test out the code, I put together a quick set of layered histograms for global real GDP per capita growth rates from 1951 to 2010. Result...
The number of countries for which data is available varies from around 50 in 1951 to roughly 190 in 2010. Perhaps this means I should have normalized the above histogram?
To test out the code, I put together a quick set of layered histograms for global real GDP per capita growth rates from 1951 to 2010. Result...
The number of countries for which data is available varies from around 50 in 1951 to roughly 190 in 2010. Perhaps this means I should have normalized the above histogram?
Saturday, January 12, 2013
Welfare costs of business cycles and models with heterogenous agents...
Start of quasi literature review for a heterogenous agents project I am starting in the near future. I will continue to update this post as I come across/finish reading additional papers...comments or links to important paper are welcome!
Literature:
Lucas (2003): Robert Lucas' Presidential Address given at the 2003 AEA conference in which he summarizes and defends his back-of-the-envelope calculation of the welfare costs of business cycles. Good, gentle introduction to the literature. Includes a good reference list and brief discussion of the the Krusell and Smith (2002) working paper.
Barlevy (2004):
Krusell and Smith (1998):
Literature:
Lucas (2003): Robert Lucas' Presidential Address given at the 2003 AEA conference in which he summarizes and defends his back-of-the-envelope calculation of the welfare costs of business cycles. Good, gentle introduction to the literature. Includes a good reference list and brief discussion of the the Krusell and Smith (2002) working paper.
Barlevy (2004):
This article reviews the literature on the cost of U.S. post-War business cycle fluctuations. I argue that recent work has established this cost is considerably larger than initial work found. However, despite the large cost of macroeconomic volatility, it is not obvious that policymakers should have pursued a more aggressive stabilization policy than they did. Still, the fact that volatility is so costly suggests stable growth is a desirable goal that ought to be maintained to the extent possible, just as policymakers are currently required to do under the Balanced Growth and Full Employment Act of 1978. This survey was prepared for the Economic Perspectives, a publication of the Federal Reserve Bank of Chicago.As boring an abstract as you will ever come across. Includes a nice table summarizing various estimates of the cost of business cycles.
Krusell and Smith (1998):
How do movements in the distribution of income and wealth affect the macroeconomy? We analyze this question using a calibrated version of the stochastic growth model with partially uninsurable idiosyncratic risk and movements in aggregate productivity. Our main finding is that, in the stationary stochastic equilibrium, the behavior of the macroeconomic aggregates can be almost perfectly described using only the mean of the wealth distribution. This result is robust to substantial changes in both parameter values and model specification. Our benchmark model, whose only difference from the representative-agent framework is the existence of uninsurable idiosyncratic risk, displays far less cross-sectional dispersion and skewness in wealth than U.S. data. However, an extension that relies on a small amount of heterogeneity in thrift does succeed in replicating the key features of the wealth data. Furthermore, this extension features aggregate time series that depart significantly from permanent income behavior.Krusell and Smith (1999):
We investigate the welfare effects of eliminating business cycles in a model with substantial consumer heterogeneity. The heterogeneity arises from uninsurable and idiosyncratic uncertainty in preferences and employment, where, regarding employment, we distinguish among employment and short- and long-term unemployment. We calibrate the model to match the distribution of wealth in U.S. data and features of transitions between employment and unemployment. Unlike previous studies, we study how business cycles affect different groups of consumers. We conclude that the cost of cycles is small for almost all groups and, indeed, is negative for some.Krebs (2004):
This paper analyzes the welfare costs of business cycles when workers face uninsurable idiosyncratic labor income risk. In accordance with the previous literature, this paper decomposes labor income risk into an aggregate and an idiosyncratic component, but in contrast to the previous literature, this paper allows for multiple sources of idiosyncratic labor income risk. Using the multi-dimensional approach to idiosyncratic risk, this paper provides a general characterization of the welfare cost of business cycles when preferences and the (marginal) process of individual labor income in the economy with business cycles are given. The general analysis shows that the introduction of multiple sources of idiosyncratic risk never decreases the welfare cost of business cycles, and strictly increases it if there are cyclical fluctuations across the different sources of risk. Finally, this paper also provides a quantitative analysis of multi-dimensional labor income risk based on a version of the model that is calibrated to match U.S. labor market data. The quantitative analysis suggests that realistic variations across two particular dimensions of idiosyncratic labor income risk increase the welfare cost of business cycles by a substantial amount.
I study the welfare cost of business cycles in a complete-markets economy where some people are more risk averse than others. Relatively more risk-averse people buy insurance against aggregate risk, and relatively less risk-averse people sell insurance. These trades reduce the welfare cost of business cycles for everyone. Indeed, the least risk-averse people benefit from business cycles. Moreover, even infinitely risk-averse people suffer only finite and, in my empirical estimates, very small welfare losses. In other words, when there are complete insurance markets, aggregate fluctuations in consumption are essentially irrelevant not just for the average person—the surprising finding of Lucas [Lucas, Jr., R.E., 1987. Models of Business Cycles. Basil Blackwell, New York] but for everyone in the economy, no matter how risk averse they are. If business cycles matter, it is because they affect productivity or interact with uninsured idiosyncratic risk, not because aggregate risk per se reduces welfare.Krusell et al. (2009):
We investigate the welfare effects of eliminating business cycles in a model with substantial consumer heterogeneity. The heterogeneity arises from uninsurable and idiosyncratic uncertainty in preferences and employment status. We calibrate the model to match the distribution of wealth in U.S. data and features of transitions between employment and unemployment. In comparison with much of the literature, we find rather large effects. For our benchmark model, we find welfare effects that, on average across all consumers, are of a bit more than one order of magnitude larger than those computed by Lucas [Lucas Jr., R.E., 1987. Models of Business Cycles. Basil Blackwell, New York]. When we distinguish long- from short-term unemployment, long-term unemployment being distinguished by poor (and highly procyclical) employment prospects and low unemployment compensation, the average gain from eliminating cycles is as much as 1% in consumption equivalents. In addition, in both models, there are large differences across groups: very poor consumers gain a lot when cycles are removed (the long-term unemployed as much as around 30%), as do very rich consumers, whereas the majority of consumers—the “middle class”—sees much smaller gains from removing cycles. Inequality also rises substantially upon removing cycles.The above paper has a 2002 working paper that seems to come to different conclusions about the welfare costs of business cycles. Technical appendices are also provided.
Thursday, January 3, 2013
How well do you know your utility function?
This is an excerpt from my teaching notes for an upcoming computational economics lab on the RBC model that I am teaching at the University of Edinburgh that I thought might be of more general interest (mostly because of the cool graphics!)...
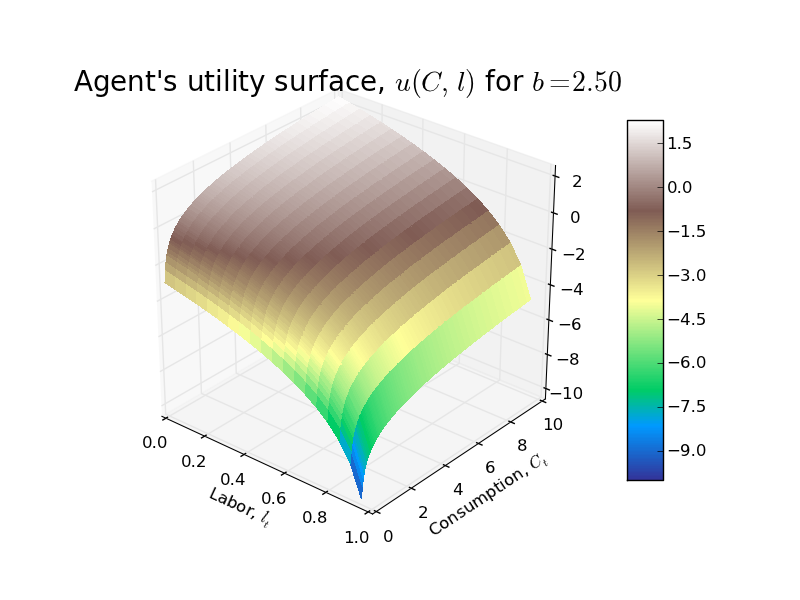
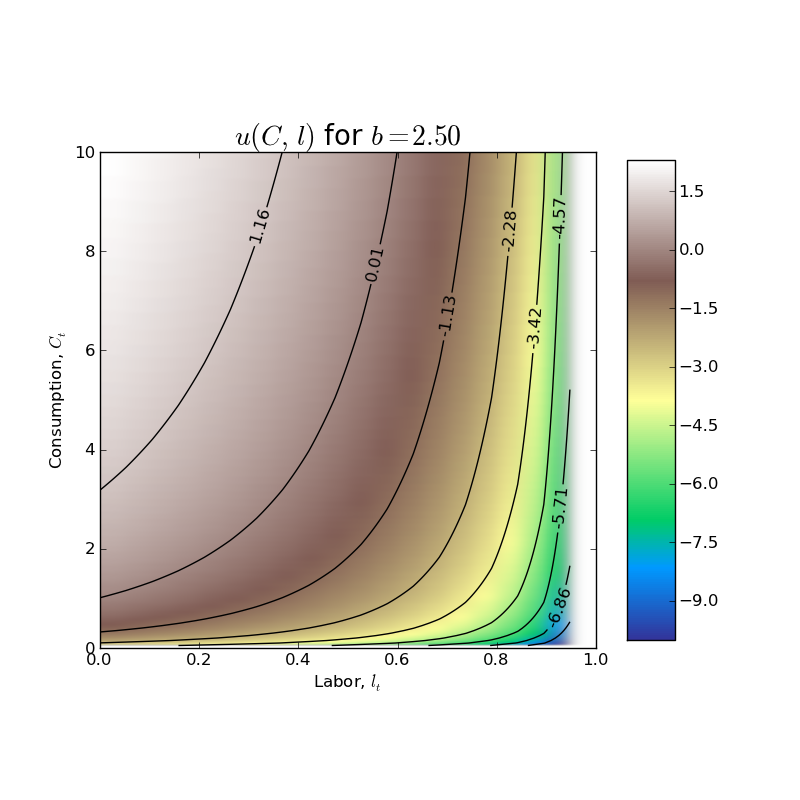
In the basic RBC model from Chapter 5 of David Romer's Advanced Macroeconomics, the representative household has the following single period utility function: $$u(C_{t}, l_{t}) = ln(C_{t}) + b\ ln(1 - l_{t})$$ where $C_{t}$ is per capita consumption, $l_{t}$ is labor (note that labor endowment has been normalized to 1!), and $b$ is a parameter (just a weight that the household places on utility from leisure relative to utility from consumption).
First a 3D plot of the utility surface...
Followed by a nice contour plot showing the indifference curves for the agent...
Suppose that the representative household lives for two periods and that there is no uncertainty about future prices. Because of logarithmic preferences, the household will follow the decision rule 'consume a fraction fixed fraction of the PDV of lifetime net worth.' We can derive this decision rule formally as follows. First, note that the household budget constraint is $$C_{0} + \frac{1}{1 + r_{1}}C_{1} = w_{0}l_{0} + \frac{1}{1 + r_{1}}w_{1}l_{1}$$ where $r_{1}$ is the real interest rate. The Lagrangian for the household's two period optimization problem is $$\max_{\{C_{t}\}, \{l_{t}\}} ln(C_{0}) + b\ ln(1-l_{0}) + \beta[ln(C_{1}) + b\ ln(1-l_{1})] + \lambda\left[w_{0}l_{0} + \frac{1}{1 + r_{1}}w_{1}l_{1} - C_{0} - \frac{1}{1 + r_{1}}C_{1}\right]$$ The household now chooses sequences of consumption and labor (i.e., representative household chooses $C_{0}, C_{1}, l_{0}, l_{1}$). The FOC along with the budget constraint imply a system of 5 equations in the 5 unknowns $C_{0}, C_{1}, l_{0}, l_{1}, \lambda$ as follows: $$\begin{align}\frac{1}{C_{0}} - \lambda =& 0 \\ \beta\frac{1}{C_{1}} - \lambda \frac{1}{1+r_{1}}=& 0 \\-\frac{b}{1 - l_{0}} + \lambda w_{0} =& 0 \\-\beta\frac{b}{1 - l_{1}} + \lambda \frac{1}{1 + r_{1}}w_{1} =& 0 \\C_{0} + \frac{1}{1 + r_{1}}C_{1} =& w_{0}l_{0} + \frac{1}{1 + r_{1}}w_{1}l_{1}\end{align}$$ This 5 equation system can be reduced (by eliminating the Lagrange multiplier $\lambda$) to a linear system of 4 equations in 4 unknowns: $$\begin{vmatrix} b & \ 0 & \ w_{0} & 0 \\\ \beta(1 + r_{1}) & -1 & 0 & 0 \\\ 0 & \ b & 0 & w_{1} \\\ 1 & \frac{1}{1 + r_{1}} & -w_{0} & -\frac{1}{1+r_{1}}w_{1} \end{vmatrix} \begin{vmatrix}C_{0} \\\ C_{1} \\\ l_{0} \\\ l_{1}\end{vmatrix} = \begin{vmatrix} w_{0} \\\ 0 \\\ w_{1} \\\ 0\end{vmatrix}$$ The above system can be solved in closde form using some method like Cramer's rule/substitution etc to yield the following optimal sequences/policies for consumption and labor supply: $$\begin{align}C_{0} =& \frac{1}{(1 + b)(1 + \beta)}\left(w_{0} + \frac{1}{1 + r_{1}}w_{1}\right) \\ C_{1} =& \left(\frac{1 + r_{1}}{1 + b}\right)\left(\frac{\beta}{1 + \beta}\right)\left(w_{0} + \frac{1}{1 + r_{1}}w_{1}\right) \\ l_{0} =& 1 - \left(\frac{b}{w_{0}}\right)\left(\frac{1}{(1 + b)(1 + \beta)}\right)\left(w_{0} + \frac{1}{1 + r_{1}}w_{1}\right) \\ l_{1} =& 1 - \left(\frac{b\beta(1+r_{1})}{w_{1}}\right) \left(\frac{1}{(1 + b)(1 + \beta)}\right)\left(w_{0} + \frac{1}{1 + r_{1}}w_{1}\right) \end{align}$$
Several important points to note about the above optimal consumption and labor supply policies:
- Household's lifetime net worth, $w_{0} + \frac{1}{1 + r_{1}}w_{1}$, is the present discounted value of its labor endowment.
- Household's lifetime net worth depends on the wages in BOTH periods and future interest rate. It hints at the more general result that, if the household has an infinite time horizon, lifetime net worth depends on the entire future path of wages and interest rates.
- In each period, household's consume a fraction of their lifetime net worth. Although the fraction changes in this simple two period model, if the household has an infinite horizon, the fraction of lifetime net worth consumed each period will be fixed and equal to $$\frac{1}{(1 + b)(1 + \beta + \beta^2 + \dots)}=\frac{1 - \beta}{1 + b}$$
- From the policy function for $l_{0}$, one can show that in order for the labor supply in period $t=0$ to be non-negative (which it must!), the following inequality must hold: $$\left(\frac{1}{1 + r_{1}}\right)\left(\frac{w_{1}}{w_{0}}\right) \lt \frac{(1 + b)(1 + \beta)}{b} - 1$$
- From the policy function for $l_{1}$, in order for the labor supply in period $t=1$ to be non-negative (which it must!), the following inequality must hold: $$(1 + r_{1})\left(\frac{w_{0}}{w_{1}}\right) \lt \left(\frac{1 + b}{b}\right)\left(\frac{1 + \beta}{\beta}\right) - 1$$
If we specify some prices (i.e., wages in period $t=0, 1$, $w_{0}=5,w_{1}=9$ and the interest rate $r_{1}=0.025$), then we can graphically represent the optimal choices of consumption and labor supply in period $t=0$ and $t=1$ as follows.
Note that with the wage in $t=1$ being almost twice as high as the wage in period $t=0$, the agent pushes his labor supply in period $t=0$, $l_{0}$, almost all the way to zero (i.e., he chooses not to work very much). The agent can still consume because, absent any frictions (things like borrowing constraints, incomplete markets, imperfect contracts, etc), he can easily consume some of his future labor earnings in period $t=1$ in the current period.
In period $t=1$, although the higher wage causes the agent to significantly increases his labor supply, there is no much change in his level of consumption (i.e., there is consumption smoothing!).
As always, code is available on GitHub.
Labels:
Graph of the Day,
matplotlib,
NumPy,
Python,
RBC Models
Python, IPython, and Emacs
For a long time now I have been meaning to move to Emacs fulltime. Today I decided to bite the bullet and dive into setting up Python, IPython, and Emacs on my MacBook. Process was surprisingly painless. Hat tip to Jess Hamrick for this very detailed post that helped get me up and running.
Wednesday, January 2, 2013
Graph of the Day
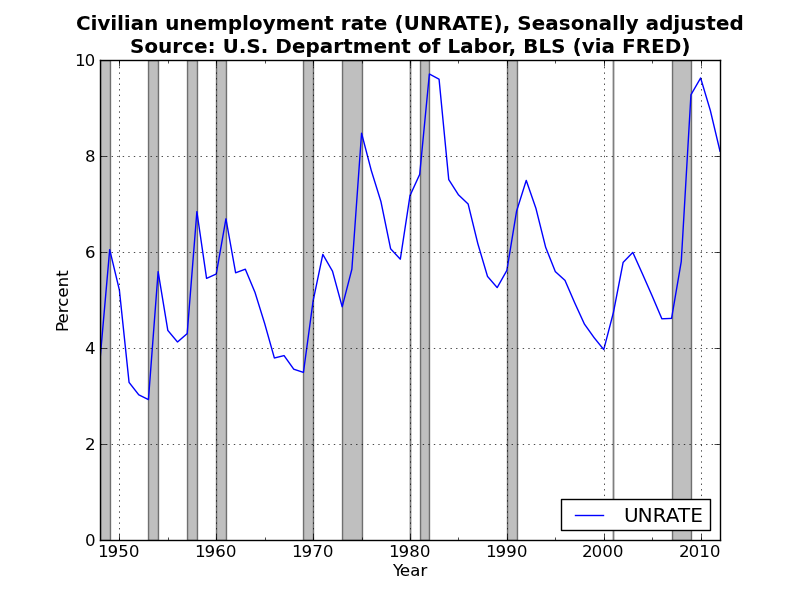
A busy day (actually trying to do a bit of my own research!)...so I just threw together a plot of the historical civilian unemployment rate using FRED data (similar to figure 1-3 from Mankiw's intermediate macroeconomics textbook). Very boring I know, but tomorrow I promise something a bit more interesting!
If anyone can point me in the direction of the actual data that Mankiw uses to generate the graphs from his textbook I would be very grateful. I can't seem to find it! Code for the above is available on GitHub.
If anyone can point me in the direction of the actual data that Mankiw uses to generate the graphs from his textbook I would be very grateful. I can't seem to find it! Code for the above is available on GitHub.
Labels:
Graph of the Day,
Macroeconomics,
matplotlib,
Pandas,
Python,
Unemployment
Tuesday, January 1, 2013
Graph of the Day
A New Year and a new graph of the day! This graphic actually uses a new Python library, wbdata, for grabbing World Bank data via the World Bank's API. Here is a plot of global inflation over the last 50 odd years for all available countries. I have color-coded the countries according to income group: Low, Lower-Middle, Upper-Middle, or High.
I am not entirely thrilled with this graph. It turned out to be hard to scale the y-axis to capture the full range of the data: Democratic Republic of Congo had an annual inflation rate over 23,000% in 1994! Zimbabwe would have had even higher annual inflation rates but they stopped reporting inflation statistics in 2006 (just prior to the onset of its recent bought of hyperinflation).
As always, code is available on GitHub.
I am not entirely thrilled with this graph. It turned out to be hard to scale the y-axis to capture the full range of the data: Democratic Republic of Congo had an annual inflation rate over 23,000% in 1994! Zimbabwe would have had even higher annual inflation rates but they stopped reporting inflation statistics in 2006 (just prior to the onset of its recent bought of hyperinflation).
As always, code is available on GitHub.
Labels:
Graph of the Day,
Inflation,
matplotlib,
Pandas,
Python,
wbdata
Subscribe to:
Posts (Atom)