Today's graphic is motivated by recent posts by Paul Krugman on implications of capital-biased technological change. In both posts Krugman uses the share of employee compensation (COE) to nominal GDP as his measure of labor's share of income. Although the data for both series go back to 1947, Krugman chooses to drop the data prior to 1973 arguing that 1973 marked the end of the post-WWII economic boom. Put another way, Krugman is saying that there is a structural break in the data generating process for labor's share which makes data prior to 1973 useless (or perhaps actively misleading) if one is interested in thinking about future trends in labor share.
If you are wondering what a plot of the entire time series looks like here is the ratio of COE / GDP from 1947 forward.
It looks like the employee compensation ratio is roughly the same today as it was in 1950 (although obviously heading in different directions!).
In his first post Krugman argues that this measure "fluctuates over the business cycle." Note that the vertical scale ranges only from 0.52 to 0.60. Such a small range will exacerbate fluctuations in the series. Plotting the same data on its natural scale (i.e., 0 to 1), yields the following.
Based on this plot, the measure appears to have been remarkably constant over the past 60 odd years.
Which of these plots gives the more "correct" view of the data? Or does it depend on the point you are trying to make?
As always, code is available.
Blog Topics...
3D plotting
(1)
Academic Life
(2)
ACE
(18)
Adaptive Behavior
(2)
Agglomeration
(1)
Aggregation Problems
(1)
Asset Pricing
(1)
Asymmetric Information
(2)
Behavioral Economics
(1)
Breakfast
(4)
Business Cycles
(8)
Business Theory
(4)
China
(1)
Cities
(2)
Clustering
(1)
Collective Intelligence
(1)
Community Structure
(1)
Complex Systems
(42)
Computational Complexity
(1)
Consumption
(1)
Contracting
(1)
Credit constraints
(1)
Credit Cycles
(6)
Daydreaming
(2)
Decision Making
(1)
Deflation
(1)
Diffusion
(2)
Disequilibrium Dynamics
(6)
DSGE
(3)
Dynamic Programming
(6)
Dynamical Systems
(9)
Econometrics
(2)
Economic Growth
(5)
Economic Policy
(5)
Economic Theory
(1)
Education
(4)
Emacs
(1)
Ergodic Theory
(6)
Euro Zone
(1)
Evolutionary Biology
(1)
EVT
(1)
Externalities
(1)
Finance
(29)
Fitness
(6)
Game Theory
(3)
General Equilibrium
(8)
Geopolitics
(1)
GitHub
(1)
Graph of the Day
(11)
Greatest Hits
(1)
Healthcare Economics
(1)
Heterogenous Agent Models
(2)
Heteroskedasticity
(1)
HFT
(1)
Housing Market
(2)
Income Inequality
(2)
Inflation
(2)
Institutions
(2)
Interesting reading material
(2)
IPython
(1)
IS-LM
(1)
Jerusalem
(7)
Keynes
(1)
Kronecker Graphs
(3)
Krussel-Smith
(1)
Labor Economics
(1)
Leverage
(2)
Liquidity
(11)
Logistics
(6)
Lucas Critique
(2)
Machine Learning
(2)
Macroeconomics
(45)
Macroprudential Regulation
(1)
Mathematics
(23)
matplotlib
(10)
Mayavi
(1)
Micro-foundations
(10)
Microeconomic of Banking
(1)
Modeling
(8)
Monetary Policy
(4)
Mountaineering
(9)
MSD
(1)
My Daily Show
(3)
NASA
(1)
Networks
(46)
Non-parametric Estimation
(5)
NumPy
(2)
Old Jaffa
(9)
Online Gaming
(1)
Optimal Growth
(1)
Oxford
(4)
Pakistan
(1)
Pandas
(8)
Penn World Tables
(1)
Physics
(2)
Pigouvian taxes
(1)
Politics
(6)
Power Laws
(10)
Prediction Markets
(1)
Prices
(3)
Prisoner's Dilemma
(2)
Producer Theory
(2)
Python
(29)
Quant
(4)
Quote of the Day
(21)
Ramsey model
(1)
Rational Expectations
(1)
RBC Models
(2)
Research Agenda
(36)
Santa Fe
(6)
SciPy
(1)
Shakshuka
(1)
Shiller
(1)
Social Dynamics
(1)
St. Andrews
(1)
Statistics
(1)
Stocks
(2)
Sugarscape
(2)
Summer Plans
(2)
Systemic Risk
(13)
Teaching
(16)
Theory of the Firm
(4)
Trade
(4)
Travel
(3)
Unemployment
(9)
Value iteration
(2)
Visualizations
(1)
wbdata
(2)
Web 2.0
(1)
Yale
(1)
Monday, December 31, 2012
Friday, December 28, 2012
Graph of the Day
Took a few days off blogging for Christmas and Boxing Day, but am now back at it! Here is a quick plot of historical measures of inflation in the U.S.. I used Pandas to grab the three price indices, and then used a nice built-in Pandas method pct_change(periods)to convert the monthly price indices (i.e., CPIAUCNS and CPIAUCSL) and the quarterly GDP deflator to measures of percentage change in prices from a year ago (which is a standard measure of inflation).
After combining the three series into a single DataFrame object, you can plot all three series with a single line of code!
Unsurprisingly the three measures track one another very closely. Perhaps I should have thrown in some measures of producer prices? Code is available here.
After combining the three series into a single DataFrame object, you can plot all three series with a single line of code!
Unsurprisingly the three measures track one another very closely. Perhaps I should have thrown in some measures of producer prices? Code is available here.
Labels:
Graph of the Day,
Inflation,
Macroeconomics,
matplotlib,
Pandas,
Python
Monday, December 24, 2012
Graph(s) of the Day!
Today's graphic(s) attempt to dispel a common misunderstanding of basic probability theory. We all know that flipping a fair coin will result in heads exactly 50% of the time. Given this, many people seem to think that the Law of Large Numbers (LLN) tells us that the observed number of heads should more or less equal the expected number of heads. This intuition is wrong!
A South African mathematician named John Kerrich was visiting Copenhagen in 1940 when Germany invaded Denmark. Kerrich spent the next five years in an interment camp where, to pass the time, he carried out a series of experiments in probability theory...including an experiment where he flipped a coin by hand 10,000 times! He apparently also used ping-pong balls to demonstrate Bayes theorem.
After the war Kerrich was released and published the results of many of his experiments. I have copied the table of the coin flipping results reported by Kerrich below (and included a csv file on GitHub). The first two collumns are self explanatory, the third column, Difference, is the difference between the observed number of heads and the expected number of heads.
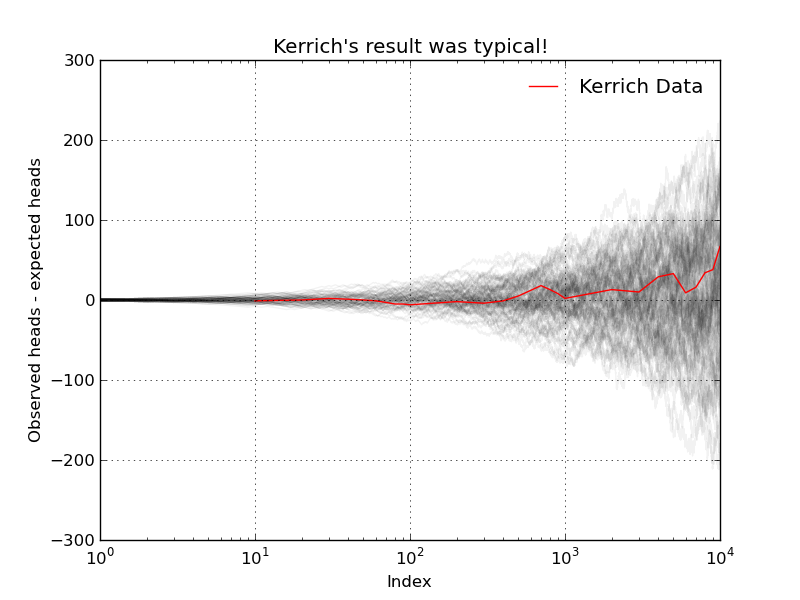
Below I plot the data in the third column: the difference between the observed number of heads and the expected number of heads is diverging (which is the exact opposite of most peoples' intuition)!
Perhaps Kerrich made a mistake (he didn't), but we can check his results via simulation! First, a single replication of T = 10,000 flips of a fair coin...
Again, we observe divergence (but this time in the opposite direction!). For good measure, I ran N=100 replications of the same experiment (i.e., flipping a coin T=10,000 times). The result is the following nice graphic...
Our simulations suggest that Kerrich's result was indeed typical. The LLN does not say that as T increases the observed number of heads will be close to the expected number of heads! What the LLN says instead is that, as T increases, the average number of heads will get closer and closer to the true population average (which in this case, with our fair coin, is 0.5).
A South African mathematician named John Kerrich was visiting Copenhagen in 1940 when Germany invaded Denmark. Kerrich spent the next five years in an interment camp where, to pass the time, he carried out a series of experiments in probability theory...including an experiment where he flipped a coin by hand 10,000 times! He apparently also used ping-pong balls to demonstrate Bayes theorem.
After the war Kerrich was released and published the results of many of his experiments. I have copied the table of the coin flipping results reported by Kerrich below (and included a csv file on GitHub). The first two collumns are self explanatory, the third column, Difference, is the difference between the observed number of heads and the expected number of heads.
| Tosses | Heads | Difference |
| 10 | 4 | -1 |
| 20 | 10 | 0 |
| 30 | 17 | 2 |
| 40 | 21 | 1 |
| 50 | 25 | 0 |
| 60 | 29 | -1 |
| 70 | 32 | -3 |
| 80 | 35 | -5 |
| 90 | 40 | -5 |
| 100 | 44 | -6 |
| 200 | 98 | -2 |
| 300 | 146 | -4 |
| 400 | 199 | -1 |
| 500 | 255 | 5 |
| 600 | 312 | 12 |
| 700 | 368 | 18 |
| 800 | 413 | 13 |
| 900 | 458 | 8 |
| 1000 | 502 | 2 |
| 2000 | 1013 | 13 |
| 3000 | 1510 | 10 |
| 4000 | 2029 | 29 |
| 5000 | 2533 | 33 |
| 6000 | 3009 | 9 |
| 7000 | 3516 | 16 |
| 8000 | 4034 | 34 |
| 9000 | 4538 | 38 |
| 10000 | 5067 | 67 |
Perhaps Kerrich made a mistake (he didn't), but we can check his results via simulation! First, a single replication of T = 10,000 flips of a fair coin...
Again, we observe divergence (but this time in the opposite direction!). For good measure, I ran N=100 replications of the same experiment (i.e., flipping a coin T=10,000 times). The result is the following nice graphic...
Our simulations suggest that Kerrich's result was indeed typical. The LLN does not say that as T increases the observed number of heads will be close to the expected number of heads! What the LLN says instead is that, as T increases, the average number of heads will get closer and closer to the true population average (which in this case, with our fair coin, is 0.5).
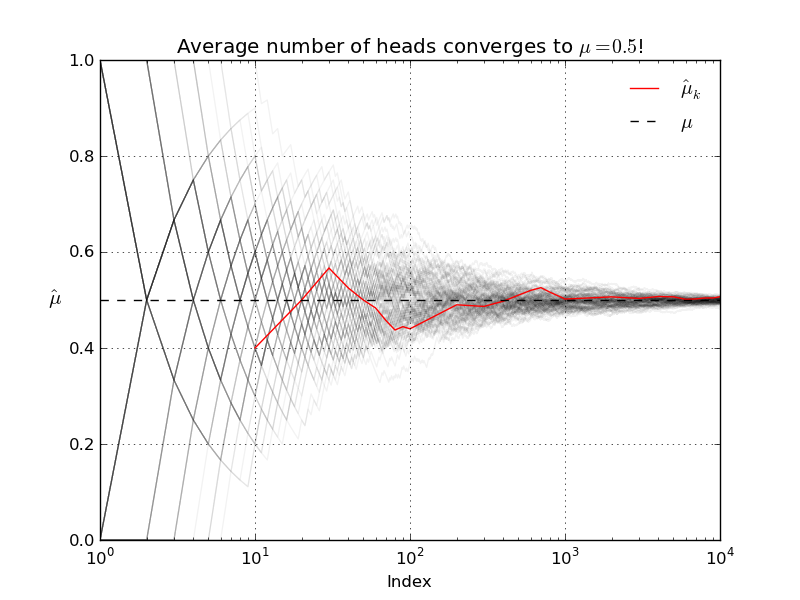
Let's run another simulation to verify that the LLN actually holds. In the experiment I conduct N=100 runs of T=10,000 coin flips. For each of the runs I re-compute the sample average after each successive flip.
As always code and data are available! Enjoy.
Labels:
Graph of the Day,
matplotlib,
NumPy,
Pandas,
SciPy,
Statistics
Sunday, December 23, 2012
Graph of the Day
Earlier this week I used Pandas to grab some historical data on the S&P 500 from Yahoo!Finance and generate a simple time series plot. Today, I am going to re-examine this data set in order to show the importance of scaling and adjusting for inflation when plotting economic data.
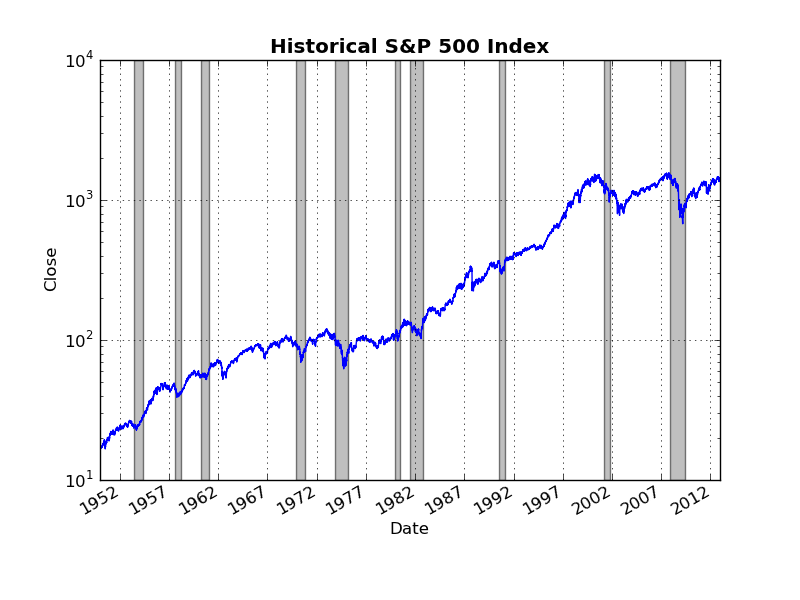
I again use the functions from the pandas.io.data to grab the data. Specifically, I use get_data_yahoo('^GSPC') to get the S&P 500 time series, and get_data_fred('CPIAUCSL')to grab the consumer price index (CPI). Here is a naive plot of historical S&P 500 returns from 1950 through 2012 (as usual, includes grey NBER recession bands).
Note that, because the CPI data are monthly frequency, I resample the daily S&P 500 data by taking monthly averages. This plot might make you conclude that there was a massive structural break/regime change around the year 2000 in whatever underlying process is generating the S&P 500. However, as the level of the S&P 500 increases, the linear scale on the vertical axis makes changes from month to month seem more dramatic. To control for this, I simply make the vertical scale logarithmic (now equal distances on the vertical axis represent equal percentage changes in the S&P 500).
Now the "obvious" structural break in the year 2000 no longer seems so obvious. Indeed there was a period of roughly 10-15 years during the late 1960's through 1970's during which the S&P 500 basically moved sideways in a similar manner to what we have experienced during the last 10+ years.
This brings us to another, more significant, problem with these graphs: neither or them adjusts for inflation! When plotting long economic time series it is always a good idea to adjust for inflation. The 1970's was a period of fairly high inflation in the U.S., thus the fact that the nominal value of the S&P 500 didn't change all that much over this period tells us that, in real terms, the value of the S&P 500 fell considerably.
Using the CPI data from FRED, it is straight-forward to convert the nominal value of the S&P 500 index to a real value for some base month/year. Below is a plot of the real S&P 500 (in Nov. 2012 Dollars), with a logarithmic scale on the vertical axis. As expected, the real S&P 500 declined significantly during the 1970's.
Code is available on GitHub. Enjoy!
I again use the functions from the pandas.io.data to grab the data. Specifically, I use get_data_yahoo('^GSPC') to get the S&P 500 time series, and get_data_fred('CPIAUCSL')to grab the consumer price index (CPI). Here is a naive plot of historical S&P 500 returns from 1950 through 2012 (as usual, includes grey NBER recession bands).
Note that, because the CPI data are monthly frequency, I resample the daily S&P 500 data by taking monthly averages. This plot might make you conclude that there was a massive structural break/regime change around the year 2000 in whatever underlying process is generating the S&P 500. However, as the level of the S&P 500 increases, the linear scale on the vertical axis makes changes from month to month seem more dramatic. To control for this, I simply make the vertical scale logarithmic (now equal distances on the vertical axis represent equal percentage changes in the S&P 500).
Now the "obvious" structural break in the year 2000 no longer seems so obvious. Indeed there was a period of roughly 10-15 years during the late 1960's through 1970's during which the S&P 500 basically moved sideways in a similar manner to what we have experienced during the last 10+ years.
This brings us to another, more significant, problem with these graphs: neither or them adjusts for inflation! When plotting long economic time series it is always a good idea to adjust for inflation. The 1970's was a period of fairly high inflation in the U.S., thus the fact that the nominal value of the S&P 500 didn't change all that much over this period tells us that, in real terms, the value of the S&P 500 fell considerably.
Using the CPI data from FRED, it is straight-forward to convert the nominal value of the S&P 500 index to a real value for some base month/year. Below is a plot of the real S&P 500 (in Nov. 2012 Dollars), with a logarithmic scale on the vertical axis. As expected, the real S&P 500 declined significantly during the 1970's.
Code is available on GitHub. Enjoy!
Saturday, December 22, 2012
Graph(s) of the Day
Suppose large number of identical firms in a perfectly competitive industry with constant returns to scale (CRTS) Cobb-Douglas production functions: \[Y = F(K, L) = K^{\alpha}(AL)^{1 - \alpha}\] Output, Y, is a homogenous of degree one function of capital, K, labor, L, and technology, A, is labor augmenting.
Typically, we economists model firms as choosing demands for capital and labor in order to maximize profits while taking prices as given (i.e., unaffected by the decisions of the individual firm):\[\max_{K,L} \Pi = K^{\alpha}(AL)^{1 - \alpha} - (wL + rK)\] where the prices are $1, w, r$. Note that I am following convention in assuming that the price of the output good is the numeraire (i.e., normalized to 1) and thus the real wage, $w$, and the return to capital, $r$, are both relative prices expressed in terms of units of the output good.
The first order conditions (FOCs) of a typical firms maximization problem are \[\begin{align}\frac{\partial \Pi}{\partial K}=&0 \implies r = \alpha K^{\alpha-1}(AL)^{1 - \alpha} \label{MPK}\\
\frac{\partial \Pi}{\partial L}=&0 \implies w = (1 - \alpha) K^{\alpha}(AL)^{-\alpha}A \label{MPL}\end{align}\] Dividing $\ref{MPK}$ by $\ref{MPL}$ (and a bit of algebra) yields the following equation for the optimal capital/labor ratio: \[\frac{K}{L} = \left(\frac{\alpha}{1 - \alpha}\right)\left(\frac{w}{r}\right)\] The fact that, for a given set of prices $w$, $r$, the optimal choices of $K$ and $L$ are indeterminate (any ratio of $K$ and $L$ satisfying the above condition will do) implies that the optimal scale of the firm is also indeterminate.
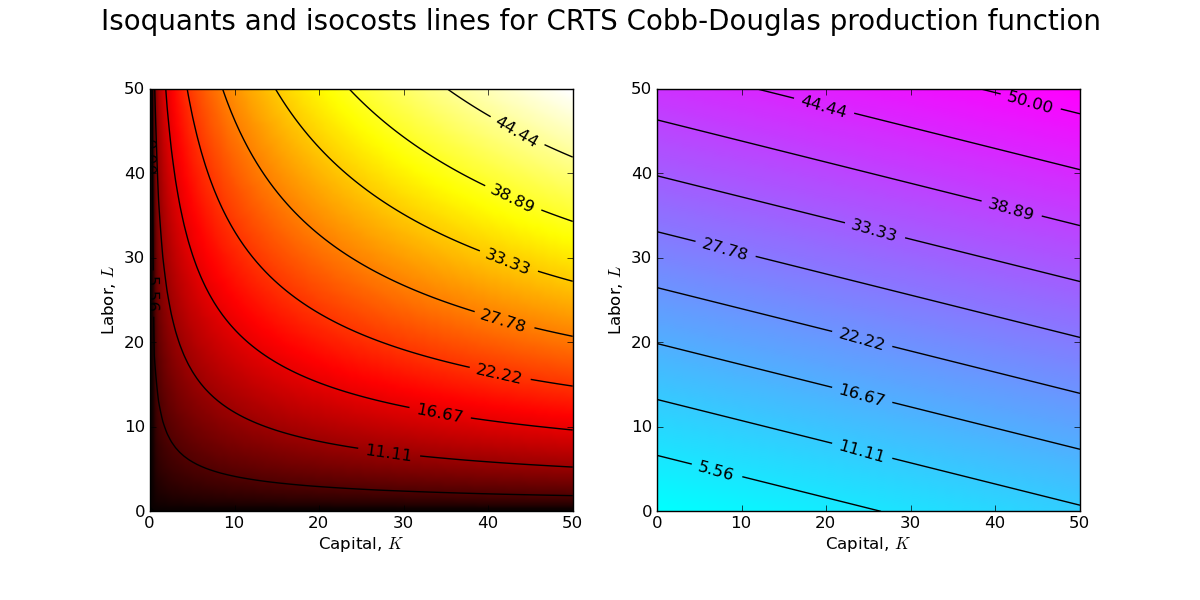
How can I create a graphic that clearly demonstrates this property of the CRTS production function? I can start by fixing values for the wage and return to capital and then creating contour plots of the production frontier and the cost surface.
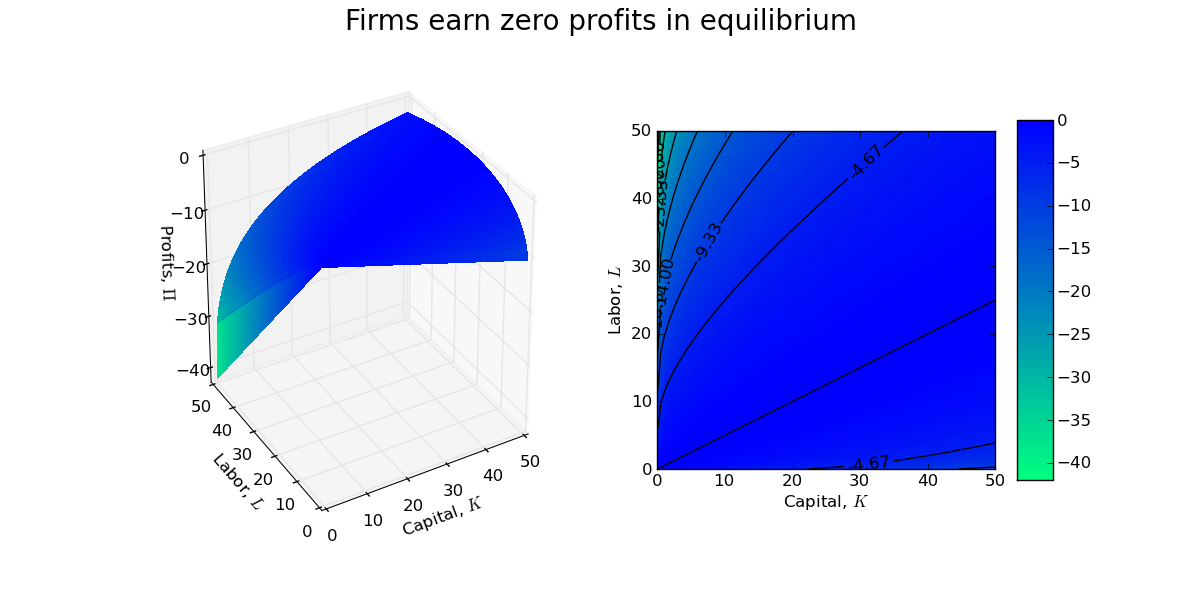
The above contour plots are drawn for $w\approx0.84$ and $r\approx0.21$ (which implies an optimal capital/labor ratio of 2:1). You should recognize the contour plot for the production surface (left) from a previous post. The contour plot of the cost surface (right) is a simple plane (which is why the isocost lines are lines and not curves!). Combining the contour plots allows one to see the set of tangency points between isoquants and isocosts.
A firm manager is indifferent between each of these points of tangency, and thus the size/scale of the firm is indeterminate. Indeed, with CRTS a firm will earn zero profits at each of the tangency points in the above contour plot.
As usual, the code is available on GitHub.
Update: Installing MathJax on my blog to render mathematical equations was easy (just a quick cut and paste job).
Typically, we economists model firms as choosing demands for capital and labor in order to maximize profits while taking prices as given (i.e., unaffected by the decisions of the individual firm):\[\max_{K,L} \Pi = K^{\alpha}(AL)^{1 - \alpha} - (wL + rK)\] where the prices are $1, w, r$. Note that I am following convention in assuming that the price of the output good is the numeraire (i.e., normalized to 1) and thus the real wage, $w$, and the return to capital, $r$, are both relative prices expressed in terms of units of the output good.
The first order conditions (FOCs) of a typical firms maximization problem are \[\begin{align}\frac{\partial \Pi}{\partial K}=&0 \implies r = \alpha K^{\alpha-1}(AL)^{1 - \alpha} \label{MPK}\\
\frac{\partial \Pi}{\partial L}=&0 \implies w = (1 - \alpha) K^{\alpha}(AL)^{-\alpha}A \label{MPL}\end{align}\] Dividing $\ref{MPK}$ by $\ref{MPL}$ (and a bit of algebra) yields the following equation for the optimal capital/labor ratio: \[\frac{K}{L} = \left(\frac{\alpha}{1 - \alpha}\right)\left(\frac{w}{r}\right)\] The fact that, for a given set of prices $w$, $r$, the optimal choices of $K$ and $L$ are indeterminate (any ratio of $K$ and $L$ satisfying the above condition will do) implies that the optimal scale of the firm is also indeterminate.
How can I create a graphic that clearly demonstrates this property of the CRTS production function? I can start by fixing values for the wage and return to capital and then creating contour plots of the production frontier and the cost surface.
The above contour plots are drawn for $w\approx0.84$ and $r\approx0.21$ (which implies an optimal capital/labor ratio of 2:1). You should recognize the contour plot for the production surface (left) from a previous post. The contour plot of the cost surface (right) is a simple plane (which is why the isocost lines are lines and not curves!). Combining the contour plots allows one to see the set of tangency points between isoquants and isocosts.
A firm manager is indifferent between each of these points of tangency, and thus the size/scale of the firm is indeterminate. Indeed, with CRTS a firm will earn zero profits at each of the tangency points in the above contour plot.
As usual, the code is available on GitHub.
Update: Installing MathJax on my blog to render mathematical equations was easy (just a quick cut and paste job).
Friday, December 21, 2012
Gun control...
Via Mark Thoma, Steve Williamson has an excellent post about the economics of gun control:
What's the problem here? People buy guns for three reasons: (i) they want to shoot animals with them; (ii) they want to shoot people with them; (iii) they want to threaten people with them. There are externalities. Gun manufacturers and retailers profit from the sale of guns. The people who buy the guns and use them seem to enjoy having them. But there are third parties who suffer. People shooting at animals can hit people. People who buy guns intending to protect themselves may shoot people who in fact intend no harm. People may temporarily feel compelled to harm others, and want an efficient instrument to do it with.
There are also information problems. It may be difficult to determine who is a hunter, who is temporarily not in their right mind, and who wants to put a loaded weapon in the bedside table.
What do economists know? We know something about information problems, and we know something about mitigating externalities. Let's think first about the information problems. Here, we know that we can make some headway by regulating the market so that it becomes segmented, with these different types of people self-selecting. This one is pretty obvious, and is a standard part of the conversation. Guns for hunting do not need to be automatic or semi-automatic, they do not need to have large magazines, and they do not have to be small. If hunting weapons do not have these properties, who would want to buy them for other purposes?
On the externality problem, we can be more inventive. A standard tool for dealing with externalities is the Pigouvian tax. Tax the source of the bad externality, and you get less of it. How big should the tax be? An unusual problem here is that the size of the externality is random - every gun is not going to injure or kill someone. There's also an inherent moral hazard problem, in that the size of the externality depends on the care taken by the gunowner. Did he or she properly train himself or herself? Did they store their weapon to decrease the chance of an accident?
What's the value of a life? I think when economists ask that question, lay people are offended. I'm thinking about it now, and I'm offended too. If someone offered me \$5 million for my cat, let alone another human being, I wouldn't take it.
In any case, the Pigouvian tax we would need to correct the externality should be a large one, and it could generate a lot of revenue. If there are 300 million guns in the United States, and we impose a tax of \$3600 per gun on the current stock, we would eliminate the federal government deficit. But \$3600 is coming nowhere close to the potential damage that a single weapon could cause. A potential solution would be to have a gun-purchaser post collateral - several million dollars in assets - that could be confiscated in the event that the gun resulted in injury or loss of life. This has the added benefit of mitigating the moral hazard problem - the collateral is lost whether the damage is "accidental" or caused by, for example, someone who steals the gun.
Of course, once we start thinking about the size of the tax (or collateral) needed to correct the inefficiency that exists here, we'll probably come to the conclusion that it is more efficient just to ban particular weapons and ammunition at the point of manufacture. I think our legislators should take that as far as it goes.
Graph of the Day
Today's graphic demonstrates the use of Pandas to grab data from Yahoo!Finance. The code I wrote uses pandas.io.get_data_yahoo() to grab historical daily data on the S&P 500 index and then generates a simple time series plot. I went ahead and added the NBER recession bars for good measure. Note the use of a logarithmic scale on the vertical axis. Enjoy!
Thursday, December 20, 2012
Graph of the Day
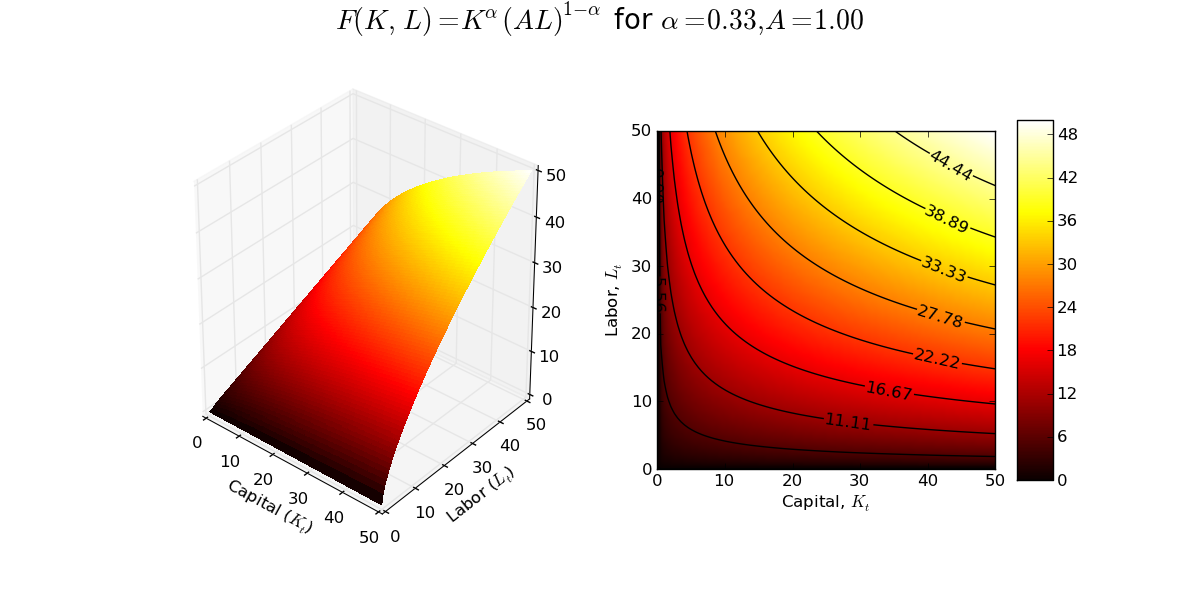
Today's graph is a combined 3D plot of the production frontier associated with the constant returns to scale Cobb-Douglas production function and a contour plot showing the isoquants of the production frontier. This static snapshot was written up using matplotlib (the code also includes an interactive version of the 3D production frontier implemented in Mayavi).
At some point I will figure out how to embed the interactive Mayavi plot into a blog post so that readers can manipulate the plot and change parameter values. If anyone knows how to do this already, a pointer would be much appreciated!
At some point I will figure out how to embed the interactive Mayavi plot into a blog post so that readers can manipulate the plot and change parameter values. If anyone knows how to do this already, a pointer would be much appreciated!
Wednesday, December 19, 2012
Blogging to resume again!
It has been far too long since my last post. Life (becoming a father), travel (summer research trip to SFI), teaching (am teaching a course on Computational Economics), and research (also trying to finish my PhD!) have a way of getting in the way of my blogging. As a mechanism to slowly move back into the blog world, I have decided to start a 'Graphic of the Day' series. Each day I will create a new economic graphic using my favorite Python libraries (mostly Pandas, matplotlib, NumPy/Scipy).
The inaugural 'Graph of the Day' is Figure 1-1 from Mankiw's intermediate undergraduate textbook Macroeconomics.
Real GDP measures the total income of everyone in the economy, and real GDP per person measures the income of the average person in the economy. The figure shows that real GDP per person tends to grow over time and that this normal growth is sometimes interrupted by period of declining income (i.e., the grey NBER bars!), called recessions or depressions.
Note that Real GDP per person is plotted on a logarithmic scale. On such a scale equal distances on the vertical axis represent equal percentage changes. This is why the distance between \$8,000 and \$16,000 (a 100% increase) is the same as the distance between \$32,000 and \$64,000 (also a 100% increase).
The Python code is available on GitHub for download (I used pandas.io.data.get_data_fred() to grab the data). The graphic is a bit boring. I was a bit depressed to find that the longest time series for U.S. per capita real GDP only goes back to 1960! This seems a bit scandalous...but perhaps I was just using the wrong data tags!
The inaugural 'Graph of the Day' is Figure 1-1 from Mankiw's intermediate undergraduate textbook Macroeconomics.
Real GDP measures the total income of everyone in the economy, and real GDP per person measures the income of the average person in the economy. The figure shows that real GDP per person tends to grow over time and that this normal growth is sometimes interrupted by period of declining income (i.e., the grey NBER bars!), called recessions or depressions.
Note that Real GDP per person is plotted on a logarithmic scale. On such a scale equal distances on the vertical axis represent equal percentage changes. This is why the distance between \$8,000 and \$16,000 (a 100% increase) is the same as the distance between \$32,000 and \$64,000 (also a 100% increase).
The Python code is available on GitHub for download (I used pandas.io.data.get_data_fred() to grab the data). The graphic is a bit boring. I was a bit depressed to find that the longest time series for U.S. per capita real GDP only goes back to 1960! This seems a bit scandalous...but perhaps I was just using the wrong data tags!
Subscribe to:
Posts (Atom)






.png)
.png)
.png)