Graph(s) of the Day!

Today's graphic(s) attempt to dispel a common misunderstanding of basic probability theory. We all know that flipping a fair coin will result in heads exactly 50% of the time.  Given this, many people seem to think that the Law of Large Numbers (LLN) tells us that the observed number of heads should more or less equal the expected number of heads. This intuition is wrong!

A South African mathematician named John Kerrich was visiting Copenhagen in 1940 when Germany invaded Denmark. Kerrich spent the next five years in an interment camp where, to pass the time, he carried out a series of experiments in probability theory...including an experiment where he flipped a coin by hand 10,000 times! He apparently also used ping-pong balls to demonstrate Bayes theorem.

After the war Kerrich was released and published the results of many of his experiments. I have copied the table of the coin flipping results reported by Kerrich below (and included a csv file on GitHub). The first two collumns are self explanatory, the third column, Difference, is the difference between the observed number of heads and the expected number of heads.

Tosses	Heads	Difference
10	4	-1
20	10	0
30	17	2
40	21	1
50	25	0
60	29	-1
70	32	-3
80	35	-5
90	40	-5
100	44	-6
200	98	-2
300	146	-4
400	199	-1
500	255	5
600	312	12
700	368	18
800	413	13
900	458	8
1000	502	2
2000	1013	13
3000	1510	10
4000	2029	29
5000	2533	33
6000	3009	9
7000	3516	16
8000	4034	34
9000	4538	38
10000	5067	67

Below I plot the data in the third column: the difference between the observed number of heads and the expected number of heads is diverging (which is the exact opposite of most peoples' intuition)! 

Perhaps Kerrich made a mistake (he didn't), but we can check his results via simulation! First, a single replication of T = 10,000 flips of a fair coin...

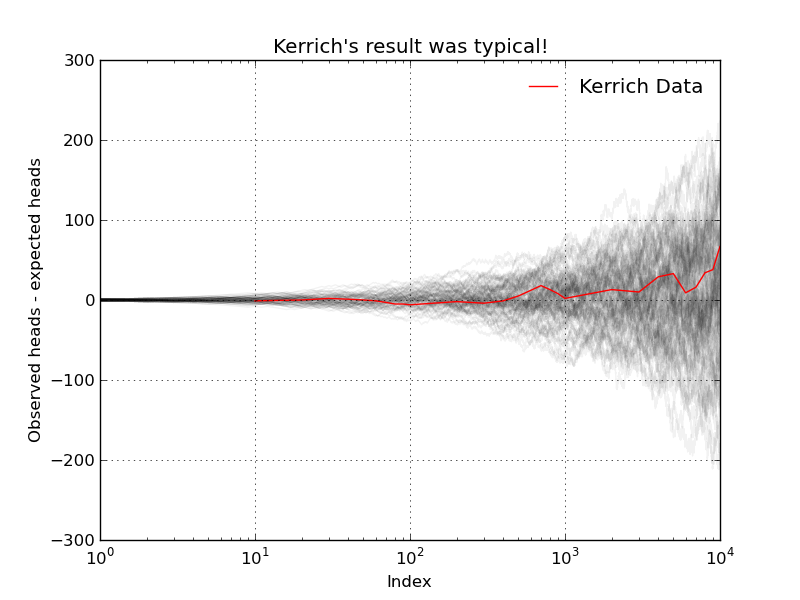
Again, we observe divergence (but this time in the opposite direction!).  For good measure, I ran N=100 replications of the same experiment (i.e., flipping a coin T=10,000 times).  The result is the following nice graphic...

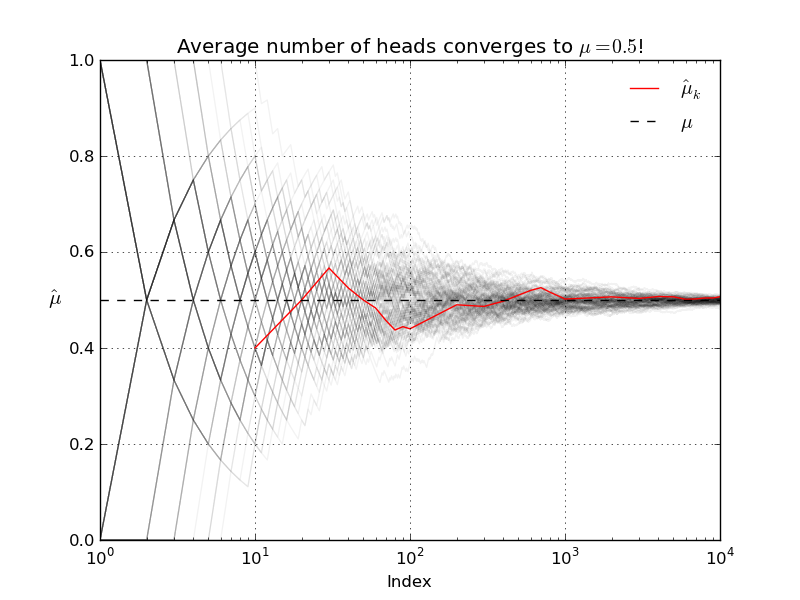
Our simulations suggest that Kerrich's result was indeed typical. The LLN does not say that as T increases the observed number of heads will be close to the expected number of heads! What the LLN says instead is that, as T increases, the average number of heads will get closer and closer to the true population average (which in this case, with our fair coin, is 0.5). 

Let's run another simulation to verify that the LLN actually holds. In the experiment I conduct N=100 runs of T=10,000 coin flips.  For each of the runs I re-compute the sample average after each successive flip.

As always code and data are available! Enjoy.